Как можно измерить глубину чего-то. Понятно, измерительным прибором. Линейкой, например, рулеткой, можно даже и веревкой. А уж коли глубина измеряемая невелика, то пальцем можно, или всей рукой. Вроде все просто и ясно. Однако могут возникать и непредвиденные трудности в измерении.
Начну с небольшого примера подобного измерения. Только измерять будем длину.
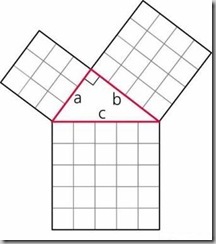
Итак, все знают, что такое прямоугольный треугольник. Многие помнят, что длина гипотенузы прямоугольного равна корню квадратному из суммы квадратов катетов. Это легендарная теорема Пифагора. Длина одного катета 3 сантиметр, второго 4 сантиметра, отсюда 9 плюс 16 равно 25. Корень квадратный из 25 равен 5. Нарисуй такой треугольник прямоугольный, и вычислять ничего не надо, меряй линейкой, не ошибешься.А подставь вместо этих значения другие. К примеру, один катет равен 4 сантиметрам, а второй пяти, чему будет равняться гипотенуза? Она есть, но вот точно измерить ее нельзя. Какой бы не была градация линейки, точно размер гипотенузы не узнаешь, измеряя ее, потому как при вычислениях по теореме Пифагора точно значения нет, цифра после запятой уходит в бесконечность. Приблизительно подсчитать и измерить можно, а вот точно никогда.
И еще один парадокс, с измерением глубины банки, наполненной концентрированной серной кислотой обыкновенной рукой. Получится ее измерить? Нет? Выходит, что банка бездонная?
О сколько нам парадоксов чудных, готовит просвещенья дух!
аха действительно парадокс!
Зачем же нужна такая точность?)
То оно только в школе в специальных задачках всегда нормальные цифры получались… А на практике оно вообще не надо…
В школе задачки все подогнаны под нормальный ответ (целые числа).
А вот насчёт неточности, которую автор заметил, то думаю, что это лишь от того, что мы (люди) не воспринимаем этот мир правильно и так далее 🙂 Возможно когда-нибудь поймём 🙂
Интересно. Действительно хороший пример.
Все в жизни относительно и литровая банка может стать бездонной и в Марианской впадине можно дно достать. Мы старательно губим нашу Землю, а она нас терпит, даеще и кормит. Парадокс не правда ли.
В жизни как раз все что угодно может пригодиться, теорема Пифагора например в строительстве или сельском хозяйстве, но естественно не всем.
проклятая математика, закончил школу пяток лет назад и всё равно она меня преследует
И вправду, некоторые недооценивают важность и значимость математики, в частности алгебры и геометрии. Та же теорема Пифагора, те же противные синусы, косинусы и тангенсы, хотя зачастую ими пользуются инженеры
Для измерения глубины нужен уровнемер, а не теорема Пифагора. Там другие законы.
Ух, сколько в математике парадоксов.
Да, надо знать что и где применяется :)) , так гораздо легче по жизни будет 😉 .
Ох же эта теорема пифагора!)) А противоречия существуют много в чем и многих ученых! И проблемы эти постоянно беспокоят математиков. Я даже скажу больше: эти проблемы и недоказанные факты постепенно решаются, доказываются… )
Fame
Это где же?)
Ха-ха, невозможность измерить рукой глубину банки с кислотой )) а как насчет померять языком температуру расплавленного свинца 😉
Да это все физика и ее премудрости и закономерности